Instructions for solving - 29th July 2012 - Little killer
Dear players of variants on sudokucup.com server. On July 29, 2012 we introduced a variant of the Little Killer.
This was the first publication of the daily variant sudoku in the league on our server, and therefore it is advisable to break down a bit, so even players who met this variant for the first time had a clue to the future, what to catch and what to concentrate in.
Have a look at the variant rules.
Today's puzzle: Little killer
rules
Write a single number from 1 to 9 in each cell such that each number appears exactly once in every row, column, and bolded 3x3 box. Numbers around the grid show sums of digits on corresponding diagonals.This Sudoku variant is often specified as a diagonal, which is not this case. Therefore, it is always good to check the assignment!
The assignment clearly shows that we have to add at the partial diagonals to go on solving. The easiest step is to fill the corners (circles in Figure 1). At two other following diagonals we can use totals that you know for example from solving of Killer Sudoku variants. But from the fourth arrow farther we have to be careful, because numbers can be repeated there! And this is also the key to solve the grid. In Figure 1 you can see the highlights of two diagonals. When you look properly, the only possibility to fill in is repeating the same numbers.
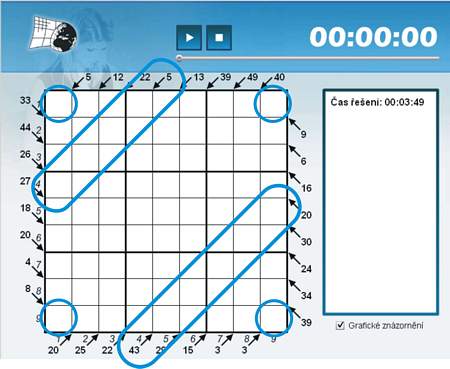
The fourth diagonal from top left should be equal to 5 and consists of 4 cells. Given that in the first square it is necessary that 2 numbers were different so it is sure that on the diagonal must necessarily lay the numbers 1, 1, 1, and 2; and 1 and 2 must lie in the second square. Likewise, in the bottom of the table at the fourth arrow from bottom there is given the sum of 43 consisting of 5 cells. This time even in the two squares (6th and 8th square) must be 2 different numbers. The highest sum of two numbers without repetition is equal to 17 (8 + 9), which gives us the sum of the 34 (17 + 17). It is therefore clear that the sum of 43 can consist of the numbers 8, 9, 9, 8, and 9.
As you can see in Figure 2, after combining known numbers that could be obtained from the surrounding arrows you can get completely filled arrows 5 and 43. And you can also see which two arrows players should focus on to find the way.
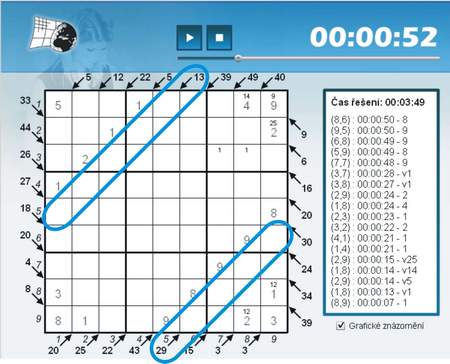
The solved diagonals can help to find numbers for adjacent diagonals. The fifth diagonal from the top left should equal 13 and consist of 5 cells and the fourth diagonal from the bottom right should be 29 in 4 cells. This time we will start in the right corner. Given that in the 6th and 8th squares numbers 8 and 9 are placed and in the 9th square there is placed number 9, we greatly narrows the number of candidates of high values from which we can take the sum of 29. If we can put no more than 7 in the 6th and 8th square, it is clear that the maximum sum is 14. For the last two cells the sum must be 15 (14 + 15 = 29), it means that there are only two possibilities 6+9 or 7+8. Without the number 9, we have only one option: 7+8. So, the sum of 29 can be composed of the numbers 7, 7, 7, and 8. Similarly, the sum of 16 must be combined of low numbers. It’s because in the 2nd and 4th square we used number 1 and in the 1st square there were used numbers 1 and 2. For more the sum must consist of 5 cells! It’s clear that the lowest sum in the 2nd and 4th square is composed of numbers 2 and 3 and its sum is 5. The rest of the sum of 13 marked at the arrow is 3, which is the number we can lay to the 1st square. Further steps are gradual developing of conditions in this task, but after finding the key steps the grid is completely open and it’s easy to finish solving.
As we showed the most important is to focus on the areas in the corners and continue from the corners towards the center. If you don’t find the shortest partial diagonals, try to focus on the interesting sums, as in this case, and try to find the key points which can “start the ball rolling”.
I hope you liked this episode of Instructions. I’ll be very happy for your feedback in our forums or on our Facebook site (http://www.facebook.com/sudokucup). There you can find the latest news and messages from the server!
And now have a look at the solving of the game from 29/07/2012 by the player with the nick of Gotroch.

