Instructions to solve Killer Sudoku of 26 December 2012

Prepared by Ondřej Suchý (nick: Čert)

 

Numbers will be written in the form: a digit in the row-column position (e.g. the digit 9 at 76 means that the digit 9 is placed in the 7th row and the 6th column).

Candidates are written in the form: a candidate in the row-column position (e.g. the candidates 12 at 89 and 99 means that the candidates 1 and 2 are placed in the 8th (respectively 9th) row and 9th column). Candidates are not surely necessary to solve sudoku, but from my own experience I know that most players use them. The candidates that are important from my point of view are underlined in the instruction.

There are used subtotals as the aid as well; they are in the form: s12 in the row-column position (e.g. s12 at 89 and 99 means that the sum of the digits put in the 8th (respectively 9th) row and 9th column is 12. These steps are helping only and they are for those players who don’t want to add up the same sums over and over again. Naturally, it isn’t necessary to mark subtotals if you want to solve that.

The steps using mainly killer sudoku rules will be explained. There won’t be explained steps using classic sudoku rules.

 

If there is written in the instruction that the sum can’t be composed of the digits, I mean that the sum can’t contain the particular digits without their recurrence – e.g. the sum of 8 can’t contain 6, it means that it isn’t possible to do that unless digit 1 is repeated in the given sum.

 

STEP BY STEP

 

1)     Using the uniqueness of the sum in particular columns/rows/squares 3x3.it is valid that the digits 1-9 appear exactly once in every column, row, and square 3x3, so the sum is 45. To understand that better – see examples in the solution below.

 

The solution:

·       8 to 49 (the sum of three cages lying mainly in the 3rd square is 53, so that in the position of 49 there must be 8 because 53 – 45 = 8)

·       6 to 61 (the sum of three cages lying mainly in the 7th square is 51, so that there must be 6 because 51 – 45 = 6)

·       3 to 96 (the sum of the cages lying in the 6th and 9th squares and of the digit 8 in the position 49 is 93. Because the forced sum of two squares is 90, it is obvious the number in the position 96 is 3)

·       9 to 14 (the sum of cages lying in the 1st and 4th squares and of the digit 6 in the position 61 is 99. Because the forced sum of two squares is 90, it is obvious the number in the position 14 is 9)

 

2)     Using of the uniqueness of the sum in particular cages (or the parts of cages). That goes that the numbers in the cages (or in their parts) can’t be repeated; look at the example – the sum of 16 in the cage with two cells can contain only the digits 7 and 9. To understand that better – see examples in the solution below.

 

·       v13 to the position 68 and 69 (the sum of two cages lying in the 6th square and of the number 8 is 41. The complement is 4, the only two digits whose sum is 4 are 1 and 3, so the forced numbers in the position 68 and 69 are 1 and 3)

·       v12 to the positions 41 and 42 (the sum of two cages lying in the 4th square and of the number 6 is 42. The complement is 3, it can be composed only of the digits 1 and 2, so the forced numbers in the position 41 and 42 are 1 and 2)

·       v789 in the positions 84, 94 and 95 (the sum 24 composed of three digits can consist only the digits 7, 8, and 9)

 

3)     Using helping sums. These steps are helpful; they are for those players who don’t want to do sums of the same digits again and again.

 

·       s12 in the positions 78 and 79 (the complement of sum of the numbers 1 and 3 in the positions 68 and 69 to 16)

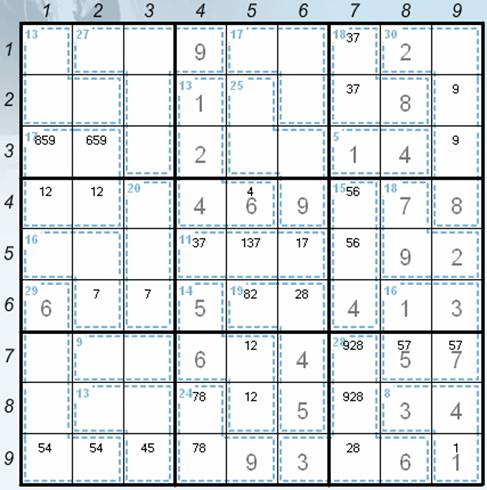
·       s14 in the positions 31 and 32 (the complement of the sum of the numbers 1 and 2 in the positions 41 and 42 to 17) – the current position – see the Picture 1.

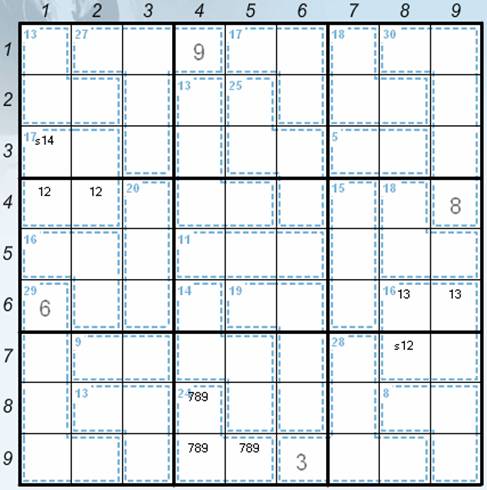
Picture 1

 

·       s15 composed of the cells in the positions 64, 65 and 66

·       s18 composed of the cells in the positions 74, 75, 76, 85 and 86

 

4)     Using sudoku rules

 

The solution:

·       9 to 95

 

5)     Adjustment of the cage candidates.

 

·       v78 to the positions 84 and 94 (the adjustment of the notes in the cage with the sum 24).

 

6)     Candidates marking

 

·       v1 to the positions 54, 55 and 56 (sudoku rules)

·       v1 to the positions 88, 89 and 99 (the digit 1 must be in the cage that contains three cells and its sum is 8)

·       v1 to the positions 17, 27 and 37 (sudoku rules)

·       v8 to the positions 17, 27 and 28 (the digit 8 can’t be in the 3rd square in the cage whose sum is 30 because of recurrence of the same digit in one cage).

·       v859 to the positions 31 and v659 to the position 32 (it is about using the sum of 14 composed of two cells and that can contain either the digits 5 and 9 or the digits 6 and 8; the digits 6 can’t be in the position 31 because it is in the position 61)

·       v9 to the positions 46 and 66 (sudoku rules, in the position 56 can’t be the digit 9 because we wouldn’t be able to make the sum of 11 with the digit 9 without recurrence of the digit 1)

·       v9 to the positions 77 and 87 (forced position of candidates, the digit 9 can’t be in the position 78 and 79 because there would be two digits 3 in one cage)

·       v9 to the positions 48, 58 and 59 (sudoku rules)

·       v6 to the positions 47 and 57 the digit 6 can’t be in the cage with the sum of 18 because the sum with the digit 9 would be possible only with the digit 3 and this is already in the 6th square in the positions 68 and 69) – the current position – see the Picture 2.

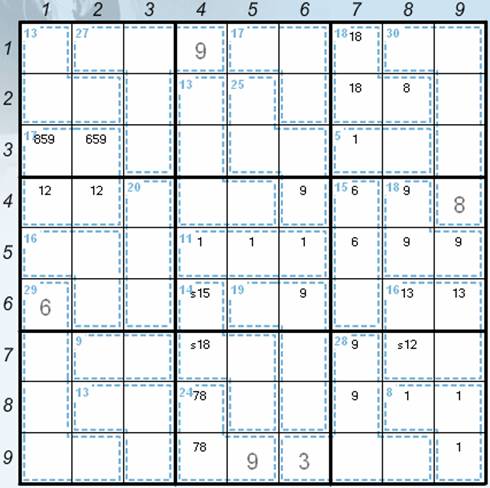
Picture 2

7)     Using sudoku and killer rules

 

The solution:

·       6 to 98 (the digit 6 can’t be in the positions 78 and 79 (the sum of 12 isn’t possible with the digit 6) and it also can’t be in the positions 88, 89 and 99 (the sum of 8 isn’t possible to compose of three digits of which one is 6)

 

8)     Candidates marking

 

·       v289 to the positions 77, 87 and 97 (the complement to the digit 9 must be two digits whose sum is 10 – the combination of the digits 1 and 9, 3 and 7, or 4 and 6 aren’t possible)

 

9)     Using sudoku and killer rules

 

The solution:

·       8 to 28 (the digit 8 can’t be in the position 18 because of recurrence of the digit in the cage)

 

10) Candidates marking

 

·       v57 to the position 78 and 79 (the only possible combination giving the sum of 12 from the remaining digits in the 9th square)

·       v3 to the position 88 and 89

 

11) Using sudoku and killer rules

 

The solution:

·       1 to 99 (using of the unique rectangle technique – the digit 1 can’t be in the positions 88 and 89; if there were the digits 1 and 3 alongside, the sudoku would have two solutions – see the positions 68, 69, 88 and 89)

 

12) Using sudoku rules

 

The solution:

·       1 to 68

·       3 to 69

·       3 to 88

·       4 to 89

 

13) Candidates marking

 

·       v5 to the positions 85 and 86 (sudoku rules)

·       v45 to the positions 91, 92 and 93 (sudoku rules)

·       v2 to the position 58 and 59 (sudoku rules)

·       v279 to the positions 48, 58 and 59 (the completion of the digit 7 to the digits 2 and 9 in the sum of 18)

·       v7 to the positions 17 and 27 (sudoku rules)

·       v378 to the positions 17 and 27 (the completion of the digit 3 to the digits 7 and 8 in the sum of 18)

 

14) Using sudoku and killer rules

 

The solution:

·       1 to 37 (the cage with the sum of 5 composed of two digits can contain in the 3rd square only digits 1 and 4, the combination of the digits 2 and 3 isn’t possible without recurrence of the digits 3 in the 3rd square; the digit 1 in the position 38 is eliminated because of sudoku rules)

·       4 to 38 (to complete the sum in the cage)

 

15) Candidates marking

 

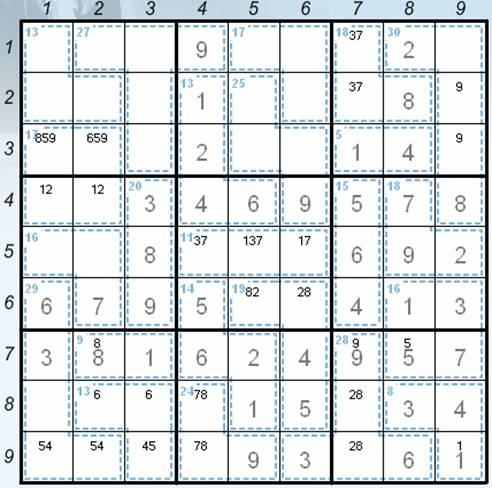
·       v456 to the positions 47, 57 and 67 (sudoku rules) – the current position – see the Picture 3.

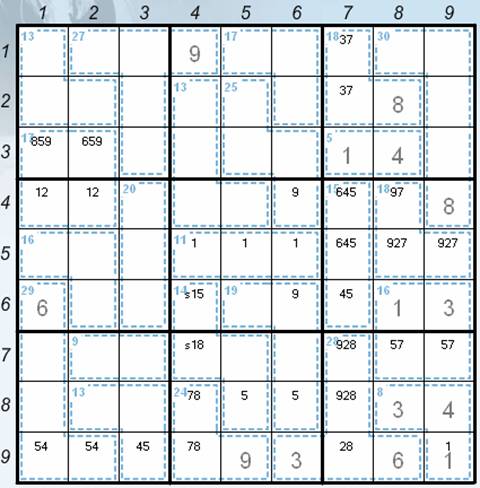
Picture 3

 

16) Using uniqueness of the sum in the cage

 

The solution:

1 to 24 (the digit 1 must be in the cage with the sum of 13 composed of four digits, it’s because the sum of four digits without the digit 1 will always be 14 at least (2 + 3 + 4 + 5 = 14)

 

17) Candidates marking and changes

 

·       v1 to the positions 55 and 56 (removal of v1 from the position 54)

·       v9 to the positions 29 and 39 (sudoku rules)

·       v27 in the position 59 (removal of v9 from the position 59)

·       v2 to the position 64, 65 and 66 (sudoku rules – see the cells 41, 42, 58 and 59)

·       v258 to the positions 64, 65 and 66 (the digit 8 must be in the positions 64, 65 and 66 – it can’t be in the cage with the sum of 11 placed in the 5th square; the digit 5 is the complement of the digits 2 and 8 to the sum of 15). This is one of the most important steps.

 

18) Using sudoku and killer rules

 

The solution:

·       4 to 67 (sudoku rules)

·       9 to 46 (9 can’t be in the position 59)

·       7 to 48 (sudoku rules)

·       9 to 58 (sudoku rules)

·       2 to 59 (sudoku rules)

·       2 to 18 (sudoku rules)

·       5 to 78 (sudoku rules)

·       7 to 79 (sudoku rules)

 

19) Candidates marking and changes

 

·       v56 to the positions 47 and 57 (candidates changes – removal of v4)

·       v7 to the positions 62 and 63 (sudoku rules) – the current position – see the Picture 4.

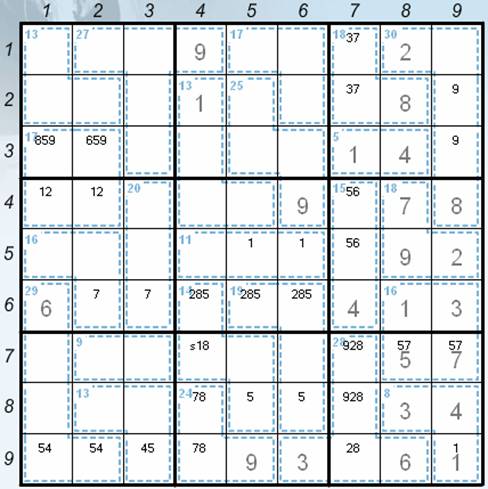
Picture 4

·       v7 to the positions 54, 55 and 56 (sudoku rules)

·       v3 to the positions 54 (the digit 3 is the complement of the digits 1 and 7 to the sum of 11), v137 to the position 55, v17 to the position 56

·       v46 to the position 44 and 45

 

20) Using sudoku and killer rules

 

The solution:

·       2 to 34 (the digit 2 is the complement of the digits 1, 4 and 6 to the sum of 13)

·       5 to 64 (sudoku rules)

·       5 to 86 (sudoku rules + elimination of the digit 5 from the position 85 because of the recurrence of the digit 5 in one cage)

·       4 to 76 (the digit 4 is the complement of the digits 2, 5 and 8 to the sum of 19)

·       4 to 44 (sudoku rules)

·       6 to 45 (sudoku rules)

·       6 to 74 (sudoku rules)

 

21) Candidates marking and change

 

·       v28 to the positions 65 and 55 (candidates change)

·       v12 to the position 75 and 85 (sudoku rules) – the current position – see the Picture 5.

Picture 5

·       v18 to the positions 72 and 73 (the sum is 9 – the combinations of the digits 2 and 7, 3 and 6 or 4 and 5 aren’t possible)

·       v6 to the positions 82 and 83 (sudoku rules)

 

22) Using sudoku and killer rules

 

The solution:

·       2 to 75 (sudoku rules)

·       1 to 85 (sudoku rules)

·       9 to 77 (sudoku rules)

·       3 to 71 (sudoku rules)

·       5 to 47 (sudoku rules)

·       6 to 57 (sudoku rules)

·       3 to 43 (sudoku rules)

·       7 to 62 (the digit 7 can’t be in the position 63 because of the sum of the cage)

·       9 to 63 (sudoku rules)

·       8 to 53 ((the digit 8 is the complement of the digits 3 and 9 to the sum of 20)

·       8 to 72 (sudoku rules)

·       1 to 73 (sudoku rules) – the current position – see the Picture 6.

 

Picture 6

 

 

23) Candidates marking and change

 

·       v45 to the positions 51 and 52 (sudoku rules)

 

24) Using sudoku and killer rules

 

The solution:

·       5 to 93 (the sum of 13 in the 7th square can be composed only as the combination of the digits 2, 5 and 6. The digit 5 can be only in the position93)

 

25) Candidates marking

 

·       v26 to the position 82 and 83 (sudoku rules)

 

26) Using sudoku rules

 

The solution:

·        8 to 87 (sudoku rules)

·        2 to 97 (sudoku rules)

·        7 to 84 (sudoku rules)

·        8 to 94 (sudoku rules)

·        9 to 81 (sudoku rules)

·        7 to 91 (sudoku rules)

·        4 to 92 (sudoku rules)

·        8 to 65 (sudoku rules)

·        2 to 66 (sudoku rules)

 

 

27) Candidates marking and change

 

·       v47 to the positions 13, 23 and 33 (sudoku rules)

 

28) Using sudoku and killer rules

 

The solution:

·       4 to 51 (sudoku rules)

·       5 to 52 (sudoku rules)

·       1 to 12 (the digits 4. 7 and 9 can be completed to the sum of 27 only with the digits 1 and 6, the combination of the digits 2 and 5 is eliminated because of the digit 5 in the positions 52 and 93)

·       1 to 41 (sudoku rules)

·       2 to 42 (sudoku rules)

·       2 to 83 (sudoku rules)

·       6 to 82 (sudoku rules)

·       5 to 31 (sudoku rules)

·       9 to 32 (the complement of the digits 1, 2 and 5 to the sum of 17)

·       9 to 29 (sudoku rules)

·       5 to 19 (sudoku rules)

·       6 to 39 (sudoku rules)

·       7 to 33 (sudoku rules)

·       8 to 11 (sudoku rules)

·       8 to 36 (sudoku rules)

·       2 to 21 (sudoku rules)

·       3 to 22 (sudoku rules)

·       3 to 17 (sudoku rules)

·       7 to 27 (sudoku rules)

·       3 to 35 (sudoku rules)

·       3 to 54 (sudoku rules)

·       1 to 56 (sudoku rules)

·       7 to 55 (sudoku rules)

·       7 to 16 (sudoku rules)

·       6 to 26 (sudoku rules)

·       6 to 13 (sudoku rules)

·       4 to 15 (sudoku rules)

·       4 to 23 (sudoku rules)

·       5 to 25 (sudoku rules) – the final position – see the Picture 7.

 

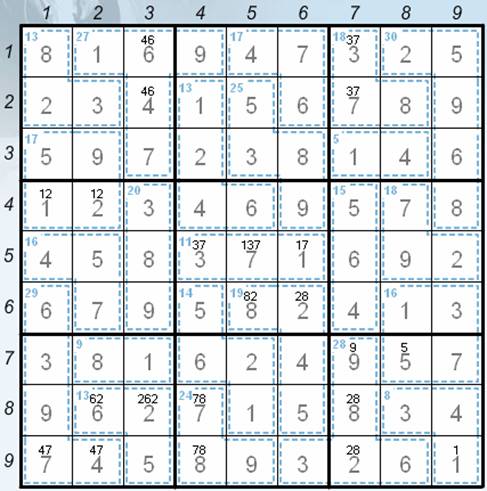
Picture 7